Archimede di Siracusa ed il calcolo del pi greco

Mura di Ortigia – Siracusa

Archimede di Siracusa è considerato oggi più che mai un genio universale, forse il più grande matematico dell'antichità e la sua grandezza fu tale che su di lui nacquero molteplici leggende nel corso dei secoli. Nato nel 287 a.C., figlio di un modesto astronomo, dedicò l'intera vita allo studio di tutte le branche della scienza di allora e fu un geniale inventore, la sua passione e la sua formazione crebbero anche a seguito di un viaggio ad Alessandria d'Egitto, allora il più importante centro scientifico del Mediterraneo. Archimede ardeva dal desiderio di conoscere, era pervaso dallo spirito della Geometria, prigioniero delle musa della conoscenza.

Archimede fu una risorsa preziosa per la sua città in tempo di pace: approfondì lo studio del funzionamento della leva (con la forza della geometria fece risparmiare molta fatica all'umanità, celebre la frase “datemi un punto d'appoggio e vi solleverò il mondo”), perfezionò la còclea o vite di Archimede, un dispositivo fatto di canali avvolti elicoidalmente attorno ad un piano inclinato, che permise di pompare grandi masse d'acqua verso l'alto, contribuendo a bonificare terre ed a prosciugare miniere. Formalizzò il principio di Archimede (o “spinta di Archimede”), una legge che riguarda i corpi immersi nei fluidi e secondo la quale un corpo immerso in un fluido riceve una spinta dal basso verso l'alto pari al peso del volume di fluido spostato. Archimede intuì tale legge immergendosi in una vasca e sentendo sul proprio corpo la spinta dell'acqua, in quel momento esclamò il celebre “Eureka!” (“ho trovato!”), Plutarco ci dice che dalla gioia se ne uscì dalla vasca e corse nudo per la città, trasmettendoci così una delle prime immagini dello scienziato distratto e con la “testa tra le nuvole”.

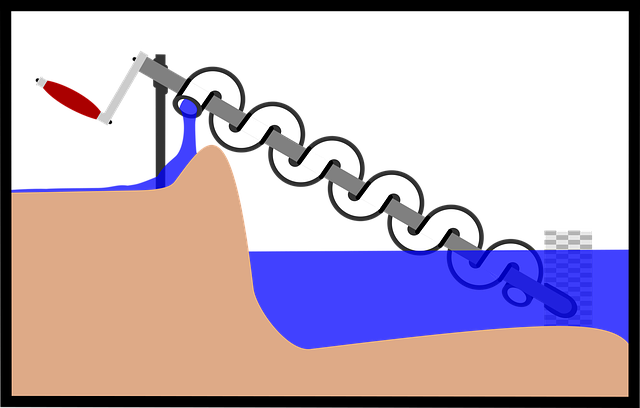
La 'vite di Archimede' per spostare l'acqua verso l'alto

Archimede costruì una sorta di planetario, un apparecchio che riproduceva il moto apparente del sole, della luna e dei pianeti; il grande sapiente dell'antichità era affascinato dalla spirale, che studiò approfonditamente, studiò aree e volumi di figure piane e solide ed il risultato del quale andava più fiero è che il volume di una sfera equivale ai 2/3 del volume del cilindro all'interno del quale essa è inscritta. Archimede inventò notazioni per numeri molto grandi e addirittura un trattato ritrovato solo nel XX secolo (“il Metodo”) evidenzia in modo stupefacente uno studioso che si confronta col concetto di infinito e con considerazioni affini al calcolo differenziale, quando ancora il mondo greco non conosceva lo zero, né i numeri irrazionali.

Archimede fu una risorsa preziosa per la greca Siracusa anche in tempo di guerra, anzi fu l'arma più potente in mano ai siracusani: la Sicilia è al centro del Mediterraneo e giocoforza si trovò coinvolta nelle guerre puniche tra Roma e Cartagine, guerre durate complessivamente 100 anni. Dopo molte discussioni interne Siracusa si schierò contro Roma: di lì a poco il generale romano Marcello attaccò la città per terra e per mare ma non fu facile averla vinta.

Archimede, già anziano, mise il suo genio al servizio della difesa della città realizzando ingegnose macchine da guerra: la leggenda vuole che inventò gli specchi ustori, scudi metallici per concentrare la luce del sole e bruciare le vele delle navi romane, realizzò una mostruosa mano di ferro, un artiglio che, mosso da carrucole, afferrava la prua delle navi, le alzava e le rilasciava bruscamente facendole rovesciare; insieme ad un sistema di balestre e catapulte che lanciavano pesanti massi dalle mura della città e dalle navi di difesa, annientò le truppe nemiche, diffondendo il terrore.

Marcello prenderà infine Siracusa, e la metterà a ferro e fuoco nel 212 a.C., dopo un assedio di ben 3 anni e, sembra, a seguito di un tradimento. Anche qui un aneddoto, forse una leggenda: Marcello aveva dato ordine di risparmiare la vita ad Archimede, sembra che un soldato romano abbia trovato Archimede intento in una dimostrazione, gli abbia ordinato di seguirlo e, dopo una risposta scocciata, lo abbia trafitto a morte.

Immagine di una macchina da guerra di Archimede – Tecnoparco Archimede Siracusa

https://www.tecnoparco-archimede.com/it/

Dell'immenso lavoro di Archimede desidero qui soffermarmi su quel numero 'magico' che oggi chiamiamo π, pi greco, esso esprime in tutti i cerchi il rapporto costante tra la circonferenza ed il diametro, sia che abbiamo a che fare con un cerchione di bicicletta, con un cartello stradale di divieto o con una ruota panoramica.

Una famosa ruota panoramica nel Prater di Vienna

Tale rapporto vale 3.141592653589793238... oggi sappiamo che π è un numero irrazionale, un numero quindi con infinite cifre decimali, senza periodicità; con l'aiuto dei computer è diventato possibile calcolare fino alla miliardesima cifra decimale, ma π continua in qualche modo a sfuggirci, si tratta di un numero al quale l'uomo non potrà mai arrivare. Ai tempi di Archimede però il calcolo del pi greco era una delle questioni matematiche sulle quali si dibatteva ed anche qui il genio siracusano diede prova della sua abilità di calcolo.

Sfruttando le scoperte del matematico-astronomo Eudosso di Cnido, allievo dell'Accademia di Platone 150 anni prima, Archimede applicò il cosiddetto 'metodo di esaustione', l'equivalente greco del moderno calcolo integrale.

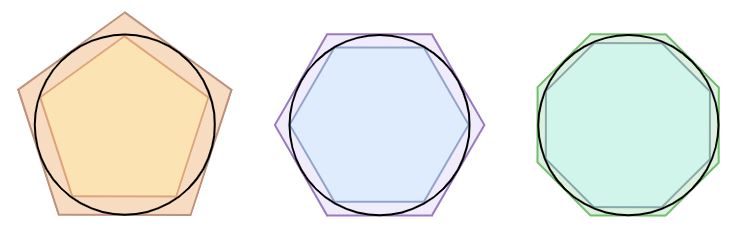
Poligoni regolari inscritti e circoscritti in un cerchio

immagine: FredrikVector: Leszek Krupinski

Questo risultato viene presentato da Archimede nel trattato 'Sulla misurazione del cerchio': i greci avevano già definito formule per calcolare il perimetro di poligoni regolari, Archimede partì da un esagono regolare inscritto in un cerchio di raggio unitario e, raddoppiando via via il numero dei lati del poligono, calcolò di volta in volta il perimetro delle figure, perimetro che si avvicinava per difetto alla misura della circonferenza. Applicò poi lo stesso procedimento anche a poligoni regolari circoscritti, cioè esterni al cerchio di raggio unitario, i cui perimetri approssimavano la circonferenza, questa volta per eccesso. Archimede calcolò fino al perimetro di due poligoni regolari con 96 lati ciascuno ed arrivò alla conclusione che il numero cercato doveva essere compreso tra 3+10/71 e 3+10/70, la miglior approssimazione mai vista fino ad allora. Il metodo di Archimede sarebbe rimasto in uso fino al 1600.

* - dvd “Giulio Giorello racconta Archimede, il primo genio universale” - collana Beautiful Minds

- “Storia della matematica” - C. B. Boyer