La geometria della natura: i frattali

Conciliare il rigore della matematica con il caos della natura non è semplice, ma grazie ai frattali la scienza è riuscita a trovare un meraviglioso punto di contatto; da qualche decennio disponiamo di nuove conoscenze, di una geometria più adeguata a descrivere le forme della natura, come le nuvole o le montagne.

Per gran parte dei 2000 anni precedenti, dopo Euclide, il presupposto prevalente è stato che per valutare gli oggetti naturali fosse possibile decostruirli trasformandoli in aggregati di figure più semplici e note, come cerchi, ellissi, poligoni, ecc., per gli oggetti bidimensionali, coni, cubi, sfere, ecc., per gli oggetti tridimensionali.  

Tuttavia, nel 1975 il matematico di origine polacca Benoît Mandelbrot, ricercatore presso IBM, attirò l'attenzione su figure non uniformi in cui si ripetono forme più grandi e forme più piccole, Mandelbrot li chiamò frattali dal latino fractus ossia “spezzato”, oggetti di dimensione anche non intera.

La sua opera innovativa poggiava sui risultati ottenuti da studiosi precedenti come quelli dei tedeschi K. Weierstrass e G. Cantor, dello svedese H. von Koch, dei francesi H. Poincaré e G. Julia e del polacco Sierpinski, tutti studi piuttosto recenti, diciamo successivi alla metà del 1800.  

Ma cosa caratterizza un oggetto frattale dal 'solito' oggetto geometrico? Gli oggetti frattali presentano auto similarità, o simmetria per dilatazione, cioè le parti che compongono la figura sono simili alla figura stessa, alla figura nel suo intero. L'aggettivo 'simili' va inteso un po' come nei triangoli, stessa forma ma dimensioni diverse. L'effetto visivo che ne consegue è legato all'invarianza di scala, in mancanza di riferimento alla scala di grandezza non riusciamo dall'immagine a distinguere se stiamo osservando un oggetto di piccole dimensioni da vicino, o uno più grande, da lontano.

Così in una spugna o in un abete o in una pianta di felce: un rametto di felce, dilatato e duplicato, si confonde con l'intera pianta, ma anche una catena montuosa ci apparirà ugualmente irregolare se la osserviamo con differenti scale, fino ad osservarne, da vicino, un singolo masso.

Sembra che la natura simpatizzi per alcune strutture, come se le avesse codificate e ripetesse alcuni schemi tante volte, in piccolo e in grande; ad esempio hanno struttura frattale i broccoli ed i cavolfiori,

Una foto di broccoli per apprezzare il concetto di auto similarità

ma anche, dentro di noi e all'interno degli animali, sono frattali organi efficientissimi come i polmoni ed i vasi sanguigni, tanta superficie in poco volume (i polmoni umani hanno la superficie di un campo da tennis in poco spazio, i vasi sanguigni raggiungono ogni angolo del nostro corpo per scambiare ossigeno e anidride carbonica ma occupano solo il 3% del volume corporeo)!

La superficie della luna? No, è mollica di pane

Attenzione, questo non significa che tutti gli oggetti siano frattali: una sedia non è formata da tante piccole sedie, ma neanche un muro di mattoni o una matrioska lo sono. Gli oggetti frattali della natura presentano auto similarità e duplicabilità di ogni loro parte e per molti livelli, i frattali della matematica invece sono dei modelli e come tali presentano auto similarità di ogni parte ma all'infinito.

Alla fine degli anni '70 Mandelbrot ha inventato un frattale denominato insieme di Mandelbrot, di bellissima complessità esso manifesta auto similarità su qualsiasi scala. L'insieme di Mandelbrot ha una struttura straordinariamente elaborata, ha un contorno assai complesso ed infinitamente contorto e se si ingrandisce una qualsiasi parte, per quanto piccola, si ottiene una copia dell'insieme stesso. L'insieme di Mandelbrot genera l'immagine di isole dal fascino barocco, in realtà determinate da una breve formula matematica z · z + c, con z e c numeri complessi e per quei punti la cui successione non diverge all'infinito.

La reiterazione opera come la ripetizione di un tema musicale, con piccole variazioni, e quello che ne esce non è ancora stato compreso appieno.

Una bella rappresentazione al computer di un “Insieme di Mandelbrot”

Diceva Mandelbrot: “il nostro cervello apprezza la ripetizione di certi schemi [...], parte della bellezza sta nel riconoscere tali schemi ripetitivi e nel comprendere che non sono perfetti”. Pittori e artisti hanno intuito e compreso tali meccanismi prima che i matematici li modellizzassero, vediamo nell'immagine seguente una delle opere del pittore giapponese Hokusai, l'occhio e la mente di Hokusai scorgevano sicuramente questi schemi nella natura.

“La grande onda di Kanagawa” - 1831 - K. Hokusai

Voglio accennare con poche immagini agli studi ai quali ha attinto Mandelbrot, prima di portarci per mano in questo nuovo mondo, è evidente che la disponibilità di computer con capacità grafiche e di linguaggi di programmazione ricorsivi hanno permesso a Mandelbrot di compiere un salto in avanti.

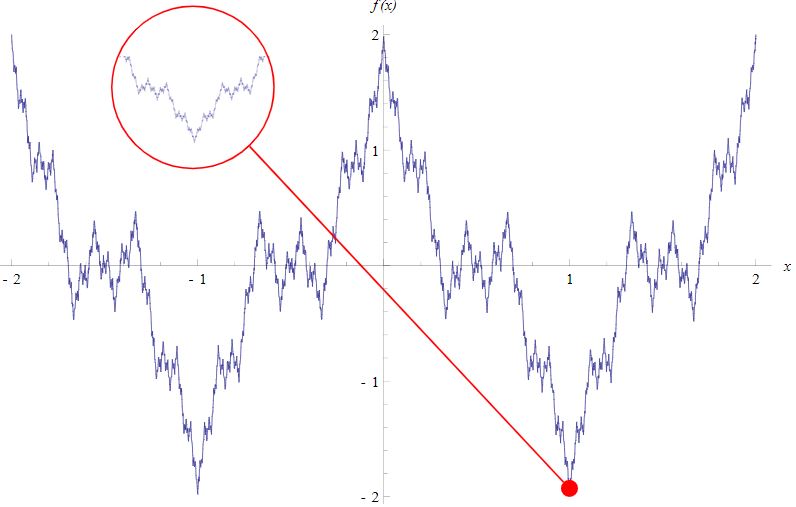
 1872 Funzione di Weierstrass

Weierstrass aveva formalizzato il concetto di 'funzione continua'. Costituita interamente da spigoli, per quanto venga ingrandita, la funzione di Weierstrass non appare mai liscia. All'epoca fu considerata un'anomalia matematica. 

1883 Insieme di Cantor  

Cantor voleva dimostrare come poter creare una linea che non fosse mai continua e avesse lunghezza zero. Costruito con l'asportazione ripetuta della terza parte centrale da una successione di linee, l'insieme di Cantor crea una serie di intervalli.

Immagine animata di Cristophe Dang Ngoc Chan

1904 Fiocco di neve di Koch

La ripetizione di un motivo triangolare con dimensioni sempre più piccole genera una figura sempre più intricata, detta curva di Koch o “fiocco di neve di Koch”.

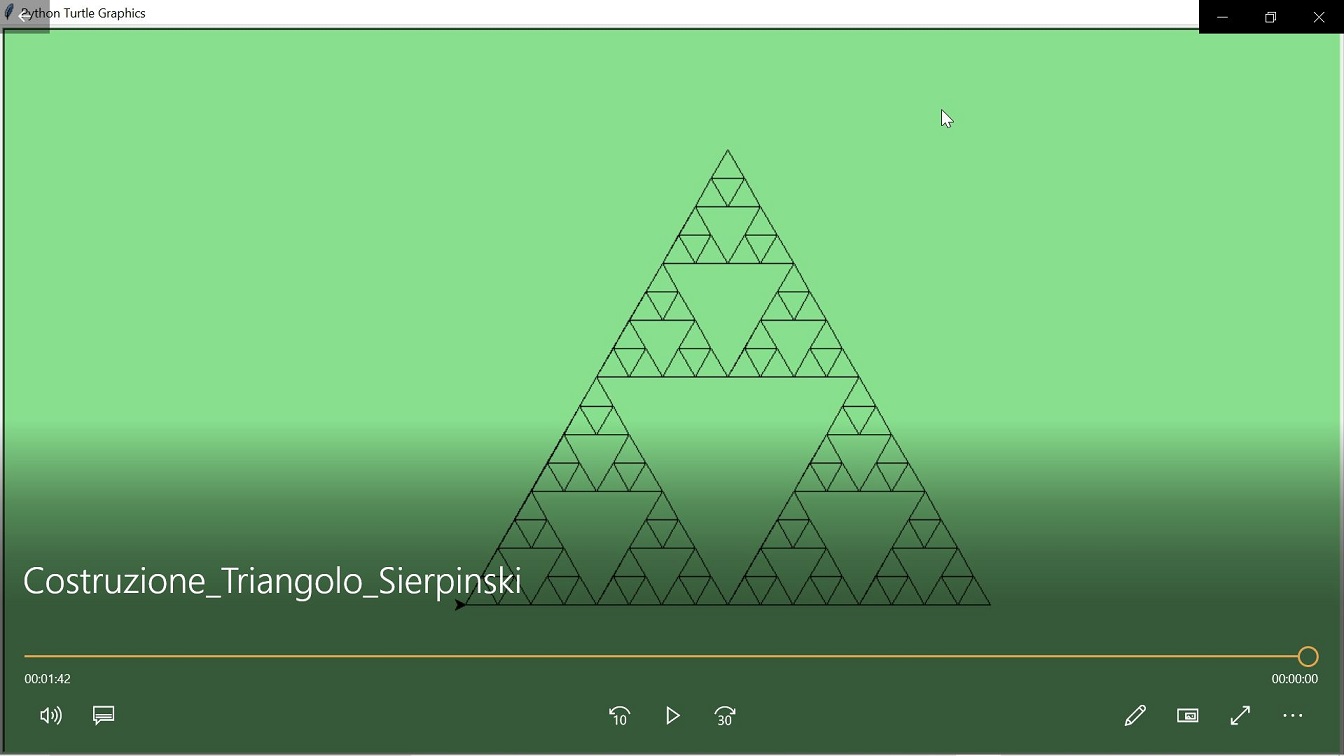
1916 Triangolo di Sierpinski

Aggiungendo triangoli dentro triangoli si crea una configurazione infinitamente merlettata. Con altro procedimento si può ottenere la figura attraverso una serie di rimozioni.

1918 Insieme di Julia

Julia studiò l’auto similarità quando cominciò a tracciare un piano complesso (il sistema di coordinate basato sui numeri complessi) immettendo un valore in una funzione, ottenendo un risultato e inserendo poi tale risultato nella funzione stessa. Julia scoprì che, dato un numero complesso, elevandolo al quadrato, sommando una costante e poi ripetendo il procedimento, alcuni valori iniziali divergevano all’infinito, altri convergevano verso un valore finito.

La geometria frattale è il principio che lega tra loro molte delle discipline di studio più rilevanti. Con i frattali la scienza è riuscita a codificare la natura in modo efficiente, a coglierne le somiglianze ed a quantificarne l'irregolarità (tecnicamente la 'dimensione frattale').

Abbiamo già discusso di alcuni aspetti legati al mondo dell'arte, la costruzione di oggetti e architetture più naturali (pensiamo alle opere di Antonio Gaudì) ci permetterebbe di vivere in un mondo ancora più bello e più in armonia con la natura. Come spesso avviene per le scoperte tecnologiche, le conseguenze sono spesso inattese: nello studio delle fluttuazioni dei mercati finanziari il diagramma dei prezzi in un secolo con rilevazioni mensili ha evidenziato sorprendenti similitudini con quello dei prezzi dell'anno, con rilevazioni ogni ora. Auto similarità!

In medicina è ovviamente fondamentale poter ricreare organi umani, ma molte sono le applicazioni dei frattali alla ricerca medica, per esempio per comprendere il comportamento dei virus e lo sviluppo dei tumori, ma anche nello studio del ritmo del cuore: l'analisi degli ECG evidenzia tutt'altro che costanza nel ritmo ma, al contrario, la presenza di continui adattamenti, irregolarità e singolarità che i frattali stanno aiutando a spiegare. L'analisi frattale viene applicata allo studio delle interruzioni di corrente nelle reti elettriche, nell'implementazione di videogiochi, in meteorologia (mai pensato che i cicloni su vasta scala, su scala molto più piccola si ripetono fino a semplici raffiche di vento?), nello sviluppo di polimeri e materiali ceramici.

Al crescere del numero delle applicazioni è sempre più evidente che i frattali ci stanno aiutando a comprendere un mondo forse solo apparentemente caotico.

 25 righe Python per ottenere quest’animazione, dimensione 500 pixel, 5 livelli

* - dvd “I frattali di Mandelbrot' – Le conquiste della matematica, formule e teorie per capire il mondo

- “Il libro della matematica. Grandi idee spiegate in modo semplice” – Gribaudo – DK

- Python Master – Linux Pro Speciale n. 24 - Sprea